Mathematische Knoten lösen

Knoten sind mathematisch interessante Objekte. Wie man sie klassifizieren kann und wie man unterschiedliche Knoten ineinander umwandeln kann, sind Fragen der topologischen Forschung. Darum geht es im weitesten Sinne auch im ERC-Grant „Cut-and-paste conjectures and multicurves”, kurz CAPCAM, von Prof. Dr. Claudius Zibrowius.

Ein Knoten besteht aus einem Stück Seil, dessen Enden miteinander verklebt sind. Mathematisch modelliert man solche Objekte als sogenannte Einbettungen vom Kreis in den drei-dimensionalen reellen Raum. Da sich Knoten nur umständlich mit Formeln beschreiben lassen, nutzen Mathematikerinnen und Mathematiker sogenannte Knotendiagramme. Dafür projizieren sie Knoten auf eine zweidimensionale Fläche – so, als würde man den Schatten abzeichnen, den ein verknotetes Seil auf ein Blatt wirft. An den Punkten, an denen sich zwei Seilstränge kreuzen, wird im Diagramm vermerkt, welcher Strang oben und welcher unten verläuft.

Wenn man an einem solchen Punkt die Stränge vertauscht, also quasi einen Strang durch den anderen hindurchschiebt, ändert sich im Allgemeinen der Knoten, der durch das Diagramm beschrieben wird. Dadurch kann auch ein völlig unverknotetes Objekt, der sogenannten Unknoten, entstehen.

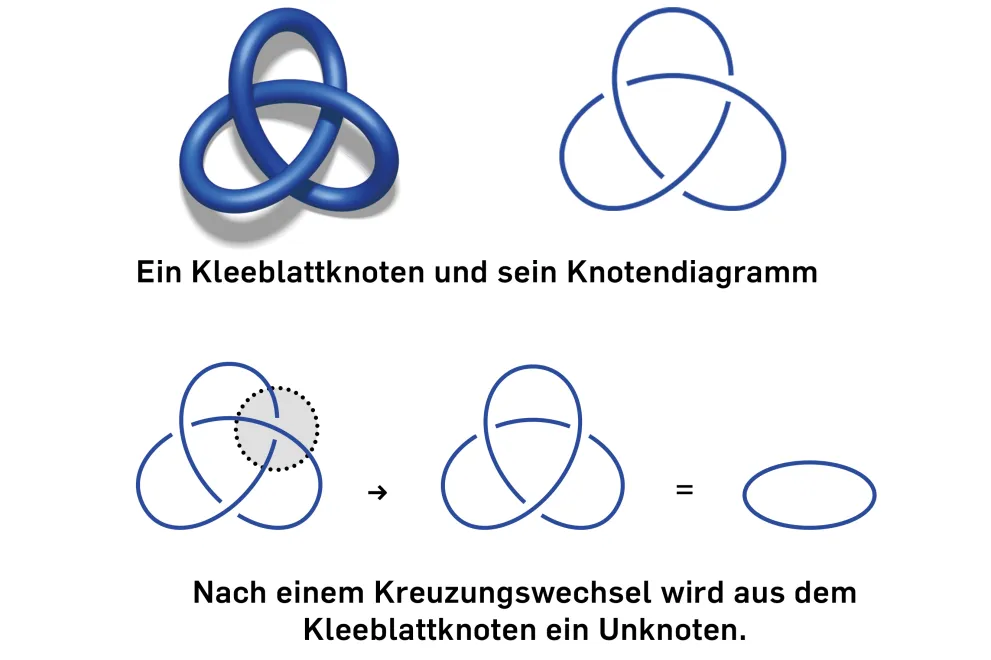
Um Knoten miteinander vergleichen zu können, suchen die Forschenden nach Invarianten, also nach Eigenschaften, die unverändert bleiben, wenn man einen Knoten verformt. Zum Beispiel hat der Unknoten die Eigenschaft, dass er eine Kreisscheibe berandet; der Kleeblattknoten hat diese Eigenschaft nicht. Der Kleeblattknoten lässt sich daher nicht in den Unknoten verformen. Die beiden Knoten sind grundlegend verschieden.

In seinem Forschungsprojekt befasst sich Claudius Zibrowius unter anderem mit der sogenannten kosmetischen Kreuzungsvermutung. Einfach ausgedrückt besagt die Vermutung, dass ein Kreuzungswechsel einen Knoten nur dann nicht grundlegend verändert, wenn er es offensichtlich nicht tut. Der mathematische Beweis dafür steht aber noch aus. Mit seinem ERC-Projekt möchte Claudius Zibrowius dazu beitragen, daran etwas zu ändern.

Der Starting Grant ist mit 1,4 Millionen Euro dotiert. Das Projekt startet 2024.